[LeetCode] 64. Minimum Path Sum - 파이썬(Python)

문제 링크 : https://leetcode.com/problems/minimum-path-sum/

Minimum Path Sum - LeetCode

유형 : 동적 계획법(Dynamic Programming)

문제 설명

음수가 아닌 숫자들로 채워진 m x n 크기의 2차원 배열 grid가 주어질 때, 왼쪽 위에서 오른쪽 아래로 이어지는 경로 중 합이 최소가 되는 경로의 합을 찾아 return 하는 문제이다. 경로를 탐색할 때는 아래 또는 오른쪽으로만 이동할 수 있다.

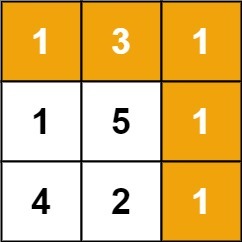
Example 1)
Input: grid = [[1,3,1],[1,5,1],[4,2,1]]
Output: 7

Example 2)
Input: grid = [[1,2,3],[4,5,6]]
Output: 12

제한사항

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 200
• 0 <= grid[i][j] <= 100

문제 풀이

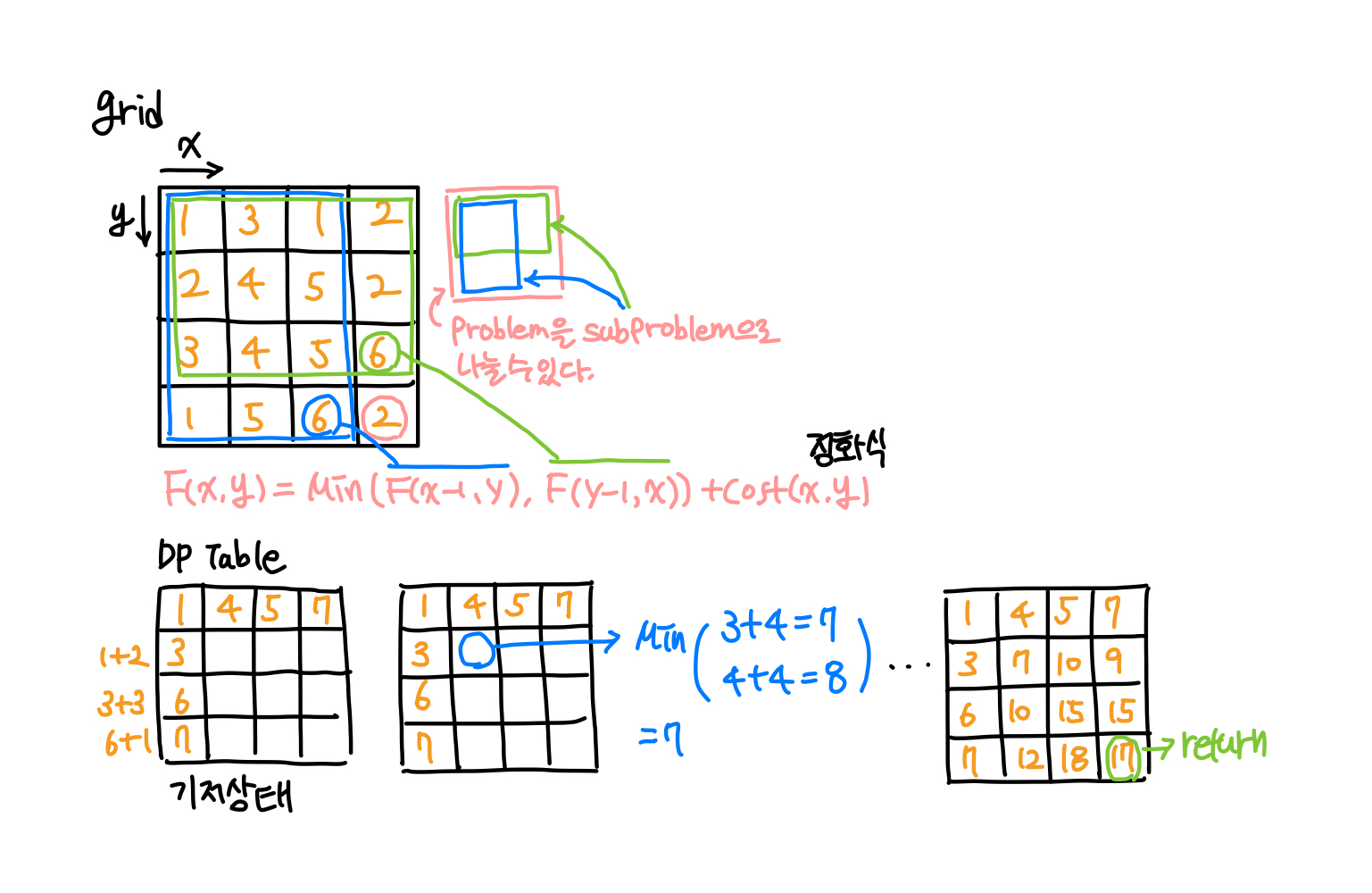
성공 코드

from typing import List

class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        rows = len(grid)
        cols = len(grid[0])
        minCost2d = a = [[0] * cols for i in range(rows)]
        
        # initialize 2d cost map
        minCost2d[0][0] = grid[0][0]
        for colIdx in range(1,cols):
            minCost2d[0][colIdx] = grid[0][colIdx] + minCost2d[0][colIdx-1]
        for rowIdx in range(1,rows):
            minCost2d[rowIdx][0] = grid[rowIdx][0] + minCost2d[rowIdx-1][0]
        
        # bottom up DP
        for rowIdx in range (1,rows):
            for colIdx in range (1,cols):
                prevCol = colIdx - 1
                prevRow = rowIdx - 1
                
                upCost = minCost2d[prevRow][colIdx]
                leftCost = minCost2d[rowIdx][prevCol]
                
                prevCost = min(upCost,leftCost)
                cost = prevCost + grid[rowIdx][colIdx]        
                minCost2d[rowIdx][colIdx] = cost
                    
        minCost = minCost2d[rows-1][cols-1]    
        return minCost

시간 복잡도 : O(m, n)

m은 grid의 행의 크기이다, n은 grid의 열의 크기이다.

공간 복잡도 : O(m, n)